ICU Physiology in 1000 Words: The Respiratory System Pressure-Volume Curve

Jon-Emile S. Kenny MD [@heart_lung]

More than 20 years ago Amato and colleagues reported a significant mortality reduction in ARDS patients who had their ventilator settings guided by the pressure-volume [PV] curve [1].  The 28-day mortality reduction was profound - 71% versus 38% - in favour of the patients who had their positive end-expiratory pressure [PEEP] set 2 cm H2O above the lower inflection point [LIP] ascertained from the PV curve.  In addition, the intervention group had their plateau pressure [Pplat] capped at 20 cm H2O.  While this trial may have been practice-changing at the time, the unusually-high mortality rate for the conventional group [i.e. 71%] coupled with simultaneous titration of PEEP and Pplat precluded definitive implementation of PV-curve-based ventilator tuning [2].  Furthermore, the landmark ARDSNet trial [3] swiftly followed as the fountainhead for modifying lung volume and airway pressure in the ARDS patient.

The Curve Basics

The PV curve is typically measured without an esophageal balloon meaning that the relationship is an amalgam of the lung and chest wall together – the ‘respiratory system.’  As pressure rises on the x-axis, volume follows on the y-axis as a function of the respiratory system compliance [see figure 1A].  Classically, the curve is measured at zero PEEP, forming a sigmoid shape because of lung recruitment at low pressure-volume and hyperinflation at high pressure-volume.  In other words, at low pressure-volume, there is a lower inflection point [LIP] created by alveolar opening pressure.  Below the LIP, there is little volume change on the y-axis; however, after the LIP pressure investment, volume rises.  Initially, the LIP was thought to be the end of alveolar recruitment and PEEP was set 2 cm H2O above this level.

Figure 1: A - cartoon of typical respiratory system compliance curve with upper inflection point [UIP] and lower inflection point [LIP] marked. Hysteresis is marked by red-dotted line. B - shows the effect of a respiratory system with increasing flow applied, note how LIP increases with increasing flow. The equation of motion below shows that pressure will increase with increasing flow. Vt is tidal volume, Crs is respiratory system compliance curve, V-dot is flow and Rrs is resistance of the respiratory system. To obtain static values, V-dot should be very low or zero.To the contrary, the upper inflection point [UIP] reveals the moment when increased airway pressure no longer raises volume on the y-axis.  The UIP was felt to mark the moment of alveolar over-distension; ergo, safe ventilation was bounded between the LIP and UIP.

Conspicuously, there is a pressure difference between inflation and deflation in the pressure volume curve; this is known as ‘hysteresis’ and occurs primarily because inflation pressure must overcome the attraction between water molecules at the water-air interface.  Surfactant mitigates inter-molecular attraction of water such that as pressure falls on deflation a larger volume is achieved [4].  For simplicity of discussion, only inflation PV curves will be considered herein; this should not, however, belie the importance of the deflation limb [5, 6].

Measuring the Curve

The point of the PV curve is to provide information on the static characteristics of the respiratory system.  Thus, like an end-inspiratory hold on a ventilator, gas flow [and patient effort] should be removed from the equation [figure 1B].  There are 3 basic techniques to measure the static pressure-volume curve: the ‘super-syringe’ method, the multiple occlusion method and the constant flow technique [4, 7].  The former two may be thought of as a series of ‘end-inspiratory’ holds – such that measurements are made at zero airflow, while the latter allows for a constant, low-flow during measurement.  Consequentially, gas flows less than 10 L/min [8, 9] should be used to mitigate the effects of dynamic airway pressure, yet even flow values less than 2 L/min can have small effects on the LIP of the PV curve [10]!

Curve Caveats

Even if the PV curve of the respiratory system is measured perfectly, there can be significant variability of LIP measurement between observers [11, 12].  Moreover, in the absence of an esophageal balloon, the chest wall contribution is ignored which may be important in the obese and/or extra-pulmonary ARDS [13, 14].  Further, patients must be deeply sedated and, potentially, paralyzed to ensure that no respiratory effort contributes to airway pressure.  Lastly, animal, clinical and mathematical models have suggested continuous recruitment of alveoli along the inflation curve beyond the LIP; conversely, some alveoli may reach their strain limit before the UIP [15-18].  Indeed, Venegas et al. found that the derivative of the equation of best-fit for the PV curve was Gaussian, suggesting a broad distribution of alveolar recruitment along the entire curve [18].

Recent Data

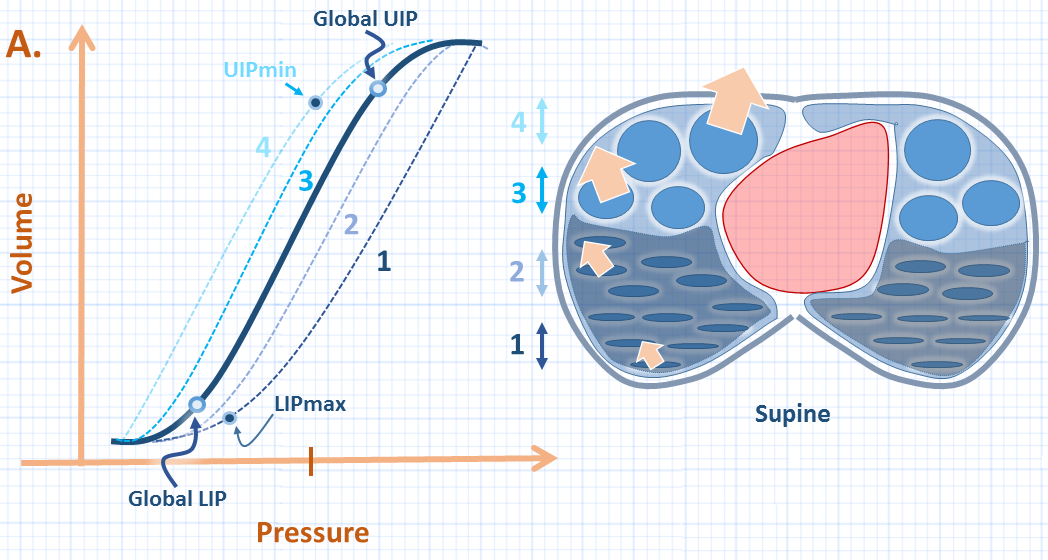
In line with the mathematical models of Venegas and Hickling [5, 16, 18], a recent and inspiring clinical study has shown that regional PV curves exist within the lung and distribute around the global PV curve [19] [see figure 2A].  Scaramuzzo and colleagues studied 41 PV curves from 12 patients with acute respiratory failure with or without ARDS.  The patients were deeply sedated and pharmacologically paralyzed in the supine position; electrical impedance tomography [EIT] was used to measure regional volumes along the ventral-dorsal axis.

In brief, the global PV curve had an LIP lower than that of the opening pressure required to open the dorsal-most lung units; thus, if the global LIP were used, the dependent lung may still act as ‘stress raisers’ – aggravating the risk of atelectrauma.  Conversely, the global UIP was found to be higher than the regional UIP of the ventral-most lung units, placing these units at risk for over-distension if the global UIP is used to limit end-inspiratory pressure.  This has implications for the ‘stress index;’ as described previously, the global UIP marks the point at which the pressure-time curve bends towards the pressure axis [i.e. stress index > 1].  Accordingly, at a stress index of exactly 1, some of the ventral-most lung units may be over-distended.  Previous data has suggested that the stress index may result in slight over-application of PEEP [20, 21].

Figure 2A: Illustration of global PV curve [dark blue] and series of regional PV curves [1-4]. The global LIP [lower inflection point] pressure is less than the LIPmax which is the highest LIP representing the dorsal-most [series 1] lung units. Thus, higher pressure is required to open these units than determined by the global curve. The upper inflection point [UIP] global is greater than the UIPmin or minimum UIP which is seen regionally in the ventral-most unit [series 4] - these units are at risk for over-distension if the global UIP is targeted.

Lastly, one may theorize how pronation may affect the regional versus global PV curves [figure 2B].  The prone position shifts the chest wall PV curve rightwards, and also ‘stiffens’ the chest wall [i.e. change its slope] [22].  With simultaneous homogenization of the pulmonary parenchyma in the prone position [23, 24], one would expect the regional curves to cluster more closely around the global curve.

Figure 2B: Theoretical change in global and regional PV curves in response to prone. Note that the UIPmin rises towards the global UIP and the LIPmax falls towards the global LIP. There is a right-shift of the whole curve. The lung slice series [1-4] are the same as figure 2A, now inverted in prone. Arrows in lung represent alveolar distending pressure.

Thus, higher absolute pressures would be required with less disparity between the global and regional values – potentially making the stress index a valuable tool for titrating PEEP in the prone position.

Please check out other articles in this series,

JE

Dr. Kenny is the cofounder and Chief Medical Officer of Flosonics Medical; he is also the creator and author of a free hemodynamic curriculum at heart-lung.org

References

1. Amato, M.B.P., et al., Effect of a protective-ventilation strategy on mortality in the acute respiratory distress syndrome. New England Journal of Medicine, 1998. 338(6): p. 347-354.

2. Grinnan, D.C. and J.D. Truwit, Clinical review: respiratory mechanics in spontaneous and assisted ventilation. Critical Care, 2005. 9(5): p. 472.

3. Network, A.R.D.S., Brower RG, Matthay MA, Morris A, Schoenfeld D, Thompson BT, Wheeler A. Ventilation with lower tidal volumes as compared with traditional tidal volumes for acute lung injury and the acute respiratory distress syndrome. N Engl J Med, 2000. 342(18): p. 1301-1308.

4. Harris, R.S., Pressure-volume curves of the respiratory system. Respir Care, 2005. 50(1): p. 78-98; discussion 98-9.

5. Hickling, K.G., Best compliance during a decremental, but not incremental, positive end-expiratory pressure trial is related to open-lung positive end-expiratory pressure: a mathematical model of acute respiratory distress syndrome lungs. Am J Respir Crit Care Med, 2001. 163(1): p. 69-78.

6. Rimensberger, P.C., et al., Lung recruitment during small tidal volume ventilation allows minimal positive end-expiratory pressure without augmenting lung injury. Crit Care Med, 1999. 27(9): p. 1940-1945.

7. Bigatello, L.M., K.R. Davignon, and H.T. Stelfox, Respiratory mechanics and ventilator waveforms in the patient with acute lung injury. Respir Care, 2005. 50(2): p. 235-45; discussion 244-5.

8. Lu, Q., et al., A simple automated method for measuring pressure–volume curves during mechanical ventilation. Am J Respir Crit Care Med, 1999. 159(1): p. 275-282.

9. Bachofen, H. and J. Hildebrandt, Area analysis of pressure-volume hysteresis in mammalian lungs. J Appl Physiol, 1971. 30(4): p. 493-7.

10. Mankikian, B., et al., A new device for measurement of pulmonary pressure-volume curves in patients on mechanical ventilation. Crit Care Med, 1983. 11(11): p. 897-901.

11. Scott Harris, R., D.R. Hess, and J.G. Venegas, An objective analysis of the pressure-volume curve in the acute respiratory distress syndrome. Am J Respir Crit Care Med, 2000. 161(2): p. 432-439.

12. O'Keefe, G.E., et al., Imprecision in lower" inflection point" estimation from static pressure-volume curves in patients at risk for acute respiratory distress syndrome. Journal of Trauma and Acute Care Surgery, 1998. 44(6): p. 1064-1068.

13. Gattinoni, L., et al., Acute respiratory distress syndrome caused by pulmonary and extrapulmonary disease. Different syndromes? Am J Respir Crit Care Med, 1998. 158(1): p. 3-11.

14. De Jong, A., D. Verzilli, and S. Jaber, ARDS in Obese Patients: Specificities and Management. Critical Care, 2019. 23(1): p. 74.

15. Salmon, R., et al., Human lung pressure-volume relationships: alveolar collapse and airway closure. J Appl Physiol, 1981. 51(2): p. 353-362.

16. Hickling, K.G., The pressure–volume curve is greatly modified by recruitment: a mathematical model of ARDS lungs. Am J Respir Crit Care Med, 1998. 158(1): p. 194-202.

17. Jonson, B., et al., Pressure–volume curves and compliance in acute lung injury: evidence of recruitment above the lower inflection point. Am J Respir Crit Care Med, 1999. 159(4): p. 1172-1178.

18. Venegas, J.G., R.S. Harris, and B.A. Simon, A comprehensive equation for the pulmonary pressure-volume curve. J Appl Physiol, 1998. 84(1): p. 389-395.

19. Scaramuzzo, G., et al., Heterogeneity of regional inflection points from pressure-volume curves assessed by electrical impedance tomography. Critical Care, 2019. 23(1): p. 119.

20. Gattinoni, L., E. Carlesso, and M. Cressoni, Selecting the ‘right’ positive end-expiratory pressure level. Curr Opin Crit Care, 2015. 21(1): p. 50-57.

21. Chiumello, D., et al., Bedside Selection of Positive End-Expiratory Pressure in Mild, Moderate, and Severe Acute Respiratory Distress Syndrome*. Crit Care Med, 2014. 42(2): p. 252-264.

22. Behazin, N., et al., Respiratory restriction and elevated pleural and esophageal pressures in morbid obesity. J Appl Physiol (1985), 2010. 108(1): p. 212-8.

23. Gattinoni, L., et al., Prone position in acute respiratory distress syndrome. Rationale, indications, and limits. Am J Respir Crit Care Med, 2013. 188(11): p. 1286-1293.

24. Gattinoni, L. and M. Quintel, How ARDS should be treated. Critical Care, 2016. 20(1): p. 1.