ICU Physiology in 1000 Words: The Right Atrial Pressure Does Not Determine Cardiac Output – Part 1

Jon-Emile S. Kenny MD [@heart_lung]

It is axiomatic that association is not causation. Sometimes, however, this principle is lost in the fuliginous fog of literature and life. It feels like we’ve known all of macrohemodynamics already, known the right atrial pressure [P_ra] and cardiac output [CO], known them rounding in the evenings, mornings, afternoons, measuring them, as we do our lives with coffee spoons. But should this lead us to some overwhelming questions? Do we dare disturb the universe?

We might read or hear or say something to the effect of: “the cardiac output [CO] fell because right atrial pressure [P_ra] rose.” But is this causation or association?  Was the rising P_ra the primum movens of diminished CO, or is this statement more accurately formulated as: ‘the CO fell and P_ra rose?” In other words, the rising P_ra and falling CO were both propelled by outside forces with the P_ra and CO having no direct influence on each other.

At the bedside, distinguishing between cause and effect is important both for diagnosis and therapy. Diagnosis because P_ra is non-invasively transduced with ultrasound, for instance via the size and collapsibility of the inferior vena cava [1] and/or the Venous Excess Ultrasound Score [VExUS] [2-4]. Can these data deduce CO?  If changes in P_ra cause changes in CO, shouldn’t we then know the etiology of shock with certainty?

And this leads to therapy – if we desire to change CO, can we do so by altering P_ra? Or are CO and P_ra like a conjoined, physiological marionette, both being pulled up and down by other hemodynamic strings?

How did we get here?

There has been great interest in Guyton’s approach to hemodynamics in the intensive care unit [ICU] [5-7]. With every review, the concept of venous return [VR] is explicated as blood flow that equals CO in the steady state [8]. More specifically, VR is described by the pressure imparted upon the blood by peripheral vascular volume and capacitance [i.e., the mean systemic filling pressure, P_msf] and how the peripheral vasculature resists blood return to the right atrium [i.e., the resistance to venous return, R_vr] [6, 7, 9]. Also important in the VR equation is the P_ra itself which acts as the ‘back pressure’ to the P_msf.

The following equation arises:

\(venous~return = \frac{P_{msf}- P_{ra}}{R_{vr}} \)

What are the independent and dependent variables?

Though the VR equation above is mathematically correct, it is deceiving, especially when considering which hemodynamic variables can be clinically manipulated [i.e., independent variables] and those that are, instead, the outputs of the system [i.e., dependent variables]. Even greater confusion arises from the fact that Guyton’s VR curve has P_ra on the x-axis which is, by convention, where the independent variable is plotted. Therefore, it is understandable for the casual reader of clinical hemodynamics to consider P_ra an independent determinant of blood flow. The problem is that P_ra is not an independent determinant of blood flow.

In the VR equation above, P_msf and R_vr are independent variables whereas both P_ra and VR are dependent. This is not new information. In Guyton’s original paper in which he equated the venous return and cardiac function curves, he explained the following [10]:

“… right atrial pressure is not one of the primary determinants of cardiac output but, instead, is itself determined simultaneously along with cardiac output.”

Below, a simplified geometrical model is built from Guytonian physiology to elaborate the independent variables of the circulatory system [11]. Additionally, this model clarifies that the dependent variable is the ‘operating point’ [OP] which is composed of both CO and P_ra, simultaneously.

Simplified geometrical model

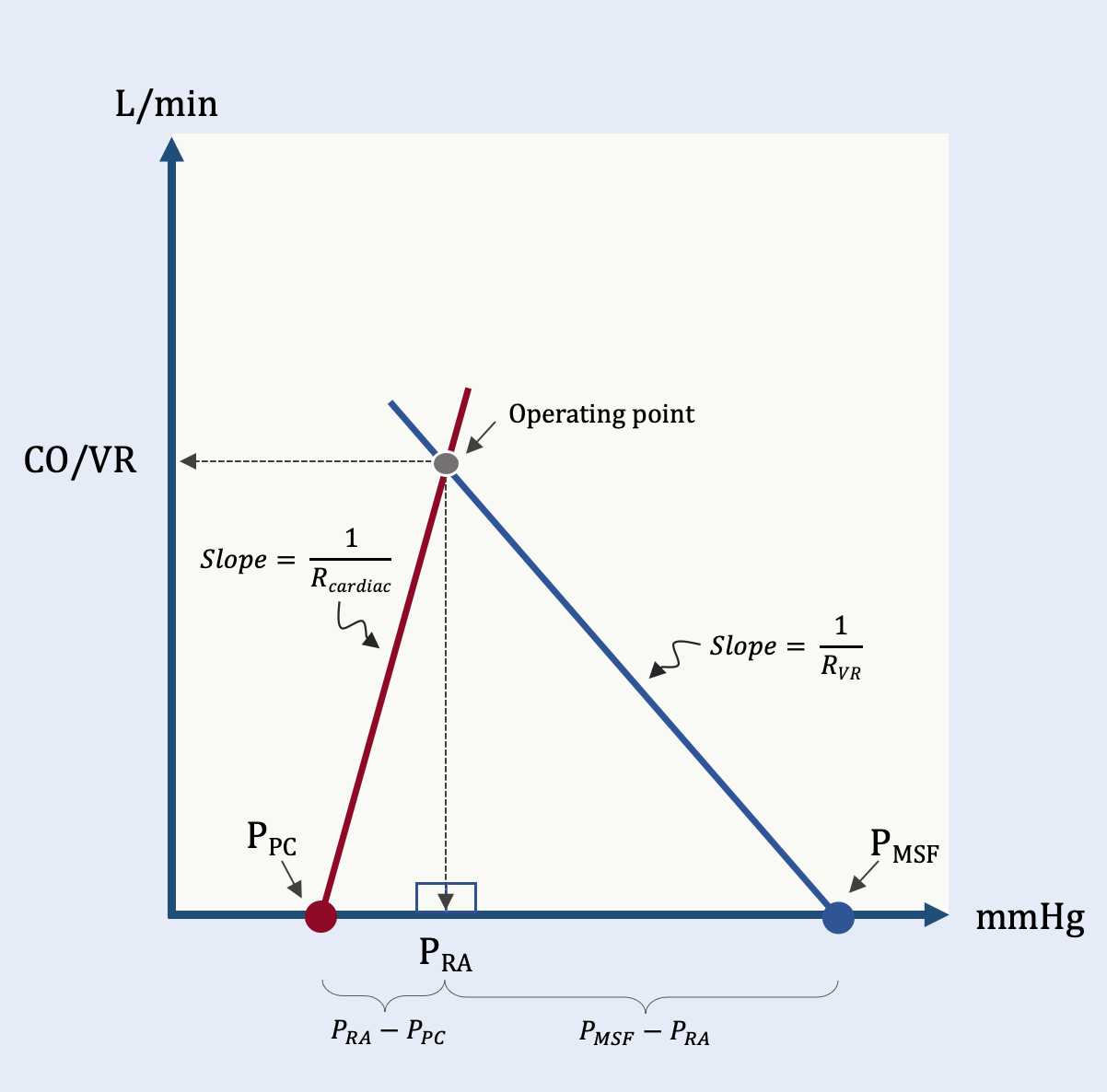
Recently, a Guyton-based model was grounded on the simple proposition that the intersection of the cardiac function and venous return curves form two adjacent right triangles [Figure 1].

Figure 1: The simplified geometrical model. The red line represents lumped cardiac function and is the hypotenuse of the ‘left’ triangle. The blue line is the resistance to venous return and the hypotenuse of the ‘right’ triangle. See text for details. The y-axis is flow in L/min and the x-axis is pressure in mmHg.

The leftmost triangle has 3 vertices: the pressure surrounding the right atrium, or the pericardial pressure (P_pc), P_ra and CO/VR. The hypotenuse of this triangle is the slope of the cardiac function curve, (1/R_cardiac). Here, R_cardiac is ‘cardiac resistance’ which is a measure of cardiac output per trans-mural pressure (i.e., P_ra less the P_pc) which is, ultimately, a measure of lumped right and left ventricular function. A high R_cardiac is diminished cardiac function while a low R_cardiac is enhanced cardiac function.

The rightmost triangle also has 3 vertices, two of which (i.e., CO/VR and P_ra) are shared with the left triangle. The final vertex of the rightmost triangle is the P_msf. The hypotenuse of this triangle is 1/R_vr which is the slope of the venous return curve. Solving simultaneous equations from both triangles simplifies to CO/VR.

\(CO/VR = \frac{P_{msf}- P_{pc}}{R_{cardiac}+R_{vr}} \)

From this, we see that P_ra is excluded from the equation; thus, P_ra is not an independent variable determining blood flow in this model. Furthermore, the equation makes explicit that there are 4 primary determinants of cardiac output: 1.) the mean systemic filling pressure; 2.) the pressure within the pericardial space, which is partly determined by pleural pressure; 3.) R_cardiac or lumped cardiac function and; 4.) the resistance to venous return, R_vr.

The dependent variable is the operating point [i.e., the shared apex of the two triangles] which contains a unique cardiac output and P_ra for the system. The system of equations above were solved for CO/VR, however, they are also solved for P_ra, below.

\(P_{ra} = \frac{P_{msf}}{ \frac{R_{vr}}{R_{cardiac}}+1} + \frac{P_{pc}}{ \frac{R_{cardiac}}{R_{vr}}+1} \)

Again, the same 4 independent variables concurrently determine P_ra as they did CO/VR. Note that this equation describes P_ra as bound between the P_msf (as an upper limit) and P_pc (as a lower limit). Whether the P_ra tilts higher towards the P_msf or lower towards the P_pc is determined by the relative values of R_vr and R_cardiac. A high R_vr and/or low R_cardiac (i.e., improved cardiac function) weights the P_ra away from the P_msf, towards the P_pc. Conversely, low R_vr and/or high R_cardiac (i.e., diminished cardiac function) pushes the P_ra upwards to the P_msf. Note, if R_cardiac is zero (i.e., perfect cardiac function), then P_ra = P_pc and if R_vr is zero, then P_ra = P_msf.

Clinical Implications

What does any of this mean?  How do the equations solving for CO/VR and P_ra help us at the bedside? Please continue reading part 2, if you dare disturb the universe.  

Best,

JE

Dr. Kenny is the cofounder and Chief Medical Officer of Flosonics Medical; he also the creator and author of a free hemodynamic curriculum at heart-lung.org.  Download his free textbook here and check out the remainder of this series.

References

1.         Kircher BJ, Himelman RB, Schiller NB: Noninvasive estimation of right atrial pressure from the inspiratory collapse of the inferior vena cava. Am J Cardiol 1990, 66(4):493-496.

2.         Longino A, Martin K, Leyba K, Siegel G, Gill E, Douglas IS et al: Correlation between the VExUS score and right atrial pressure: a pilot prospective observational study. Crit Care 2023, 27(1):205.

3.         Argaiz ER: VExUS Nexus: Bedside Assessment of Venous Congestion. Adv Chronic Kidney Dis 2021, 28(3):252-261.

4.         Beaubien-Souligny W, Rola P, Haycock K, Bouchard J, Lamarche Y, Spiegel R et al: Quantifying systemic congestion with Point-Of-Care ultrasound: development of the venous excess ultrasound grading system. The ultrasound journal 2020, 12(1):1-12.

5.         Sylvester JT, Goldberg HS, Permutt S: The role of the vasculature in the regulation of cardiac output. Clin Chest Med 1983, 4(2):111-126.

6.         Rothe CF: Physiology of venous return. An unappreciated boost to the heart. Arch Intern Med 1986, 146(5):977-982.

7.         Jacobsohn E, Chorn R, O'Connor M: The role of the vasculature in regulating venous return and cardiac output: historical and graphical approach. Can J Anaesth 1997, 44(8):849-867.

8.         Persichini R, Lai C, Teboul JL, Adda I, Guérin L, Monnet X: Venous return and mean systemic filling pressure: physiology and clinical applications. Crit Care 2022, 26(1):150.

9.         Rothe CF: Mean circulatory filling pressure: its meaning and measurement. J Appl Physiol (1985) 1993, 74(2):499-509.

10.       Guyton AC: Determination of cardiac output by equating venous return curves with cardiac response curves. Physiol Rev 1955, 35(1):123-129.

11.       Kenny JS: A framework for heart-lung interaction and its application to prone position in the acute respiratory distress syndrome. Front Physiol 2023, 14:1230654.